For Aristotle, the fundamental logical unit is the class. Classes are just sets of things—sets that we can pick out using language. The simplest way to identify a class is by using a plural noun: trees, clouds, asteroids, people—these are all classes. Names for classes can be grammatically more complex, too. We can modify the plural noun with an adjective: ‘rich people’ picks out a class. (See what I did there?) Prepositional phrases can further specify: ‘rich people from Italy’ picks out a different class. The modifications can go on indefinitely: ‘rich people from Italy who made their fortunes in real estate and whose grandmothers were rumored to be secret lovers of Benito Mussolini’ picks out yet another class—which is either very small, or possibly empty, I don’t know. (Empty classes are just classes with no members; we’ll talk more about them later.) We will refer to names of classes as ‘class-terms’, or just ‘terms’ for short. Since for Aristotle the fundamental logical unit is the class, and since terms are the bits of language that pick out classes, Aristotle’s logic is often referred to as a ‘term logic’. This is in contrast to the logic we will study in the next chapter, Sentential logic, so-called because it takes the fundamental logical unit to be the proposition, and sentences are the linguistic vehicle for picking those out. Of course, Aristotelian Logic must also deal with propositions—we’re evaluating arguments here, and by definition those are just sets of propositions—but since classes are the fundamental logical unit, Aristotle restricts himself to a particular kind of proposition: categorical propositions. ‘Category’ is just a synonym of ‘class’. Categorical propositions are propositions that make a claim about the relationship between two classes. This is the first step in taming natural language: Aristotelian Logic will only evaluate arguments made up entirely of categorical propositions. We’re limiting ourselves to a restricted portion of language—sentences expressing these kinds of propositions, which will feature two class terms—terms picking out the classes whose relationship is described in the categorical proposition. Soon, we will place further restrictions on the forms these sentences can take, but for now we will discuss categorical propositions generally. Again, categorical propositions make an assertion about the relationship between two classes. There are three possibilities here: (1) Whole Inclusion: one class is contained entirely within the other.
Example: Class 1 = people; Class 2 = bipeds. The first class is entirely contained in the second; every person is a biped. (Even amputees. Being a biped is belonging to a species that naturally has two legs.) (2) Partial Inclusion: one class is partially contained within the other; the two classes have at least one member in common. Example: Class 1 = people; Class 2 = swimmers. Some people swim; some don’t. Some swimmers are people; some aren’t (fish, e.g.). These two classes overlap, but not entirely. (3) Exclusion: the two classes don’t have any members in common; they are exclusive. Example: Class 1 = people; Class 2 = birds. No people are birds; no birds are people. Batman notwithstanding (dude’s not really a bat; also, bats aren’t birds; robins are, but again, Robin’s not actually a bird, just a guy who dresses up like one). Given these considerations, we can (more or less) formally define categorical propositions: A categorical proposition is a claim about the relationship between two classes—call them S and P—that either affirms or denies that S is wholly or partially included in P. (Note that denying that S is even partially included in P is the same as affirming that S and P are exclusive.) Aristotle noted that, given this definition, there are four types of categorical proposition. We will discuss them in turn.
Universal affirmative (A) (Since ‘Universal affirmative’—along with the names of the other three types of categorical proposition—is a bit of a mouthful, we will follow custom and assign the four categoricals (shorthand for ‘categorical propositions’) single- letter nicknames. The universal affirmative is the A proposition.) This type of proposition affirms the whole inclusion of the class S in the class P—it says that each member of S is also a member of P. The canonical expression of this proposition is a sentence of the form ‘All S are P’. It is worth noting at this point why we chose ‘S’ and ‘P’ as the symbols for generic class terms. That’s because the former is the grammatical subject (S) of the sentence, and the latter is the grammatical predicate (P). This pattern will hold for the other three types of categorical proposition. Back to the universal affirmative, A proposition. It affirms whole inclusion. For example, the sentence ‘All men are mortals’ expresses a proposition of this type, one that is true. ‘All men are Canadians’ also expresses a universal affirmative proposition, one that is false. For the sake of concreteness, let’s choose subject and predicate classes that we can use as go-to examples as we talk about each of the four types of categorical proposition. Let’s let S = logicians and P = jerks. The A proposition featuring these two classes is expressed by ‘All logicians are jerks’. (We’ll remain agnostic about whether it’s true or false.) When it comes time to test arguments for validity—the last step in the process we’ve just begun— it will be convenient for us to represent the four types of categorical propositions pictorially. The basic form of the pictures will be two overlapping circles, with the left-hand circle representing the subject class and the right-hand circle representing the predicate class. Like this: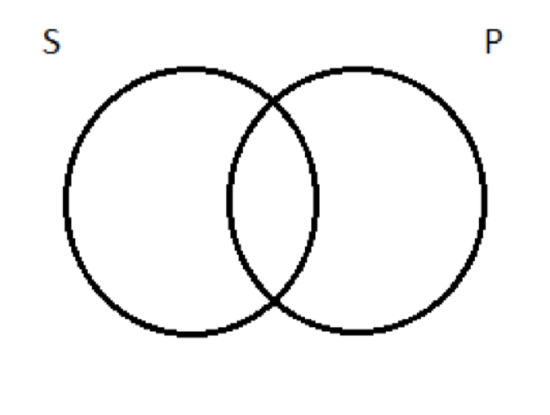 
To depict the four types of categorical propositions, we’ll modify this basic two-circle diagram by shading in parts of it or making marks inside the circles. Before we get to the specific depiction of the A proposition, though, let’s talk about what the basic two-circle diagram does. It divides the universe into four regions, to which we can assign numbers like this: 
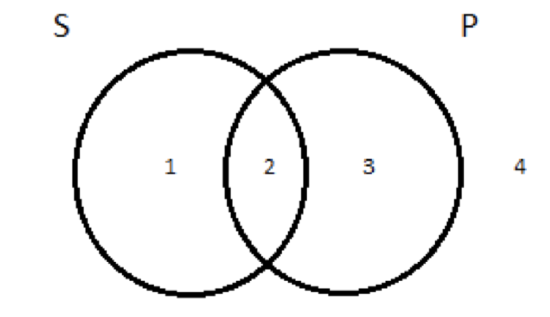Let’s talk about what’s inside each of the four regions if we take S to be the class of logicians and P to be the class of jerks. Region 1 is the portion of the S circle that doesn’t overlap with the P circle. These are things in the subject class but outside the predicate class; they are logicians who aren’t jerks. I never met him myself, but there’s no evidence in the historical record to indicate that Aristotle was anything but a gentleman. So Aristotle is one of the residents of region 1—a logician who’s not a jerk. Region 2 is the area of overlap between the subject and predicate classes; its residents are members of both. So here we have the logicians who are also jerks. Gottlob Frege, a 19th century German logician, is the most important innovator in the history of logic other than Aristotle. Also, it turns out, he was a huge jerk. He was a big-time anti-Semite. So Frege lives in region 2; he’s both a logician and a jerk. Region 3 is the portion of the P circle that doesn’t overlap with S. These are members of the predicate class—jerks, in our example—who are not members of the subject class—not logicians. This is where the non-logician jerks live. Donald Trump is a resident of region 3. The guy is clearly a jerk—and just as clearly, not a logician. (I’ve been using Trump in this example for a decade; I’m not going to stop just because he got elected president. Moreover, I take it that even Trump’s supporters would acknowledge that he’s a jerk. He tells it like it is and doesn’t care whose feelings get hurt—or something like that, right?) Region 4 is—everything else. It’s all the things that are outside both the subject and predicate classes—things that are neither logicians nor jerks. You know who seems nice, but isn’t a logician? Beyoncé. She lives in region 4. But so do lots and lots and lots of other things: the planet Jupiter is neither a logician nor a jerk; it’s in there with Beyoncé, too. As is the left-front tire of my wife’s car. And the second-smallest brick in the Great Wall of China. And so on. So much for the blank two-circle diagram and how it carves up the universe. What we want to figure out is how to alter that diagram so that we end up with a picture of the universal affirmative proposition. Our particular example of an A proposition is that all logicians are jerks. How do we draw a picture of that, using the two circles as our starting point? Well, think about it this way: when we say all logicians are jerks, what we’re really saying is that a certain kind of thing doesn’t exist; there’s no such thing as a non-jerky logician. In other words, despite what I said above about Aristotle, region 1 is empty, according to this proposition (which, again, may or may not be true; it doesn’t matter whether it’s true or not; we’re just trying to figure out how to draw a picture that captures the claim it makes). To depict emptiness, we will adopt the convention of shading in the relevant region(s) of the diagram. So our picture of the universal affirmative looks like this: 
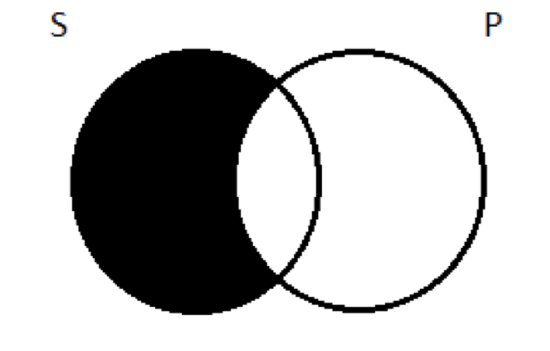All S are P means that you won’t find any members of S that are outside the P circle (no logicians who aren’t jerks). The place in the diagram where they might’ve been such things is blotted out to indicate its emptiness. The only portion of S that remains as a viable space is inside the P circle, in what we called region 2 (the logicians you do find will all be jerks). A reasonable question could be raised at this point: why did we draw the universal affirmative that way, instead of another, alternative and possibly more intuitive way? A propositions affirm whole inclusion—that S in entirely contained within P. Isn’t the obvious way to depict that state of affairs more like this: 
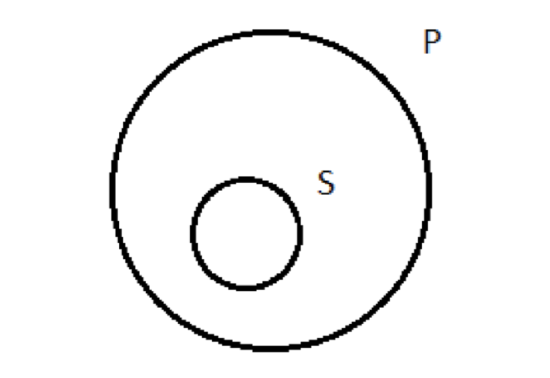S entirely contained within P. Easy. Why bother with the overlapping circles and the shading? There’s nothing wrong with this alternative depiction of the universal affirmative; it captures the claim being made. We adopt the first alternative depiction for purely practical reasons: when it comes time to test arguments for validity, we’re going to use these pictures; and our method will depend on our four types of categorical propositions all being depicted starting with the same basic two-overlapping-circle diagram, with shading and marks inside. These diagrams, as you may know, are called “Venn Diagrams”. They are named after the 19th century English logician John Venn, who invented them specifically as an easier means of testing arguments for validity in Aristotelian Logic (things were more unwieldy before Venn’s innovation). It turns out Venn’smethod only works if we start with the overlapping circles for all four of the types of categorical proposition. So that’s what we go with. Universal negative (E) This type of proposition denies that S is even partially included in P. Put another way: it affirms that S and P are exclusive—that they have no members in common. The canonical expression of this proposition is a sentence of the form ‘No S are P’. So, for example, the sentence ‘No dogs are cats’ expresses a true universal negative proposition; the sentence ‘No animals are cats’ expresses a false one. Again, we want to think about how to depict this type of proposition using the standard two-circle Venn diagram. Think about the proposition that no logicians are jerks. How do we draw a picture of this claim? Well, as we said, E propositions tell us that the two classes don’t have any members in common. The region of the two-circle diagram where there are members of both classes is the area of overlap in the picture (what we referred to as region 2 above). The universal negative proposition tells us that there’s nothing in there. So if I claim that no logicians are jerks, I’m saying that, contrary to my claims above about the jerkiness of Gottlob Frege, no, there’s no such thing as a logician-jerk. Region two is empty, and so we shade it out: 
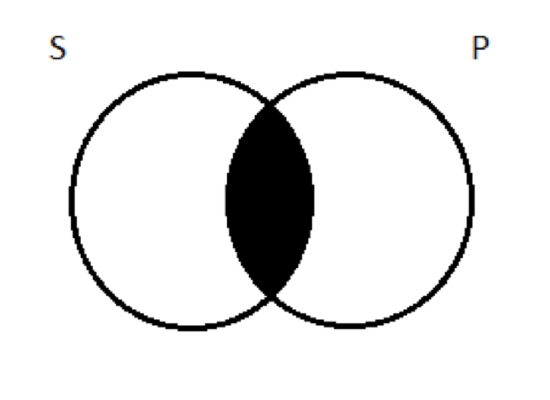Particular affirmative (I) This type of proposition affirms that S is partially included in P. Its canonical expression is a sentence of the form ‘Some S are P’. So, for example, ‘Some sailors are pirates’ expresses a true particular affirmative proposition; ‘Some sumo wrestlers are pigeons’ expresses a false one. Before we talk about how to depict I propositions with a Venn diagram, we need to discuss the word ‘some’. Remember, in Aristotelian Logic we’re taming natural language by restricting ourselves to a well-behaved portion of it—sentences expressing categorical propositions. We’re proposing to use sentences with the word ‘some’ in them. ‘Some’, however, is not particularly well-behaved, and we’re going to have to get it in line before we proceed. Consider this utterance: “Some Republican voters are gun owners.” This is true, and it communicates to the listener the fact that there’s some overlap between the classes of Republican voters and gun owners. But it also communicates something more—namely, that some of those Republicans aren’t gun owners. This is a fairly typical implicature (recall our discussion of this linguistic phenomenon in Chapter 2, when we looked at the fallacy of equivocation): when we say that some are, we also communicate that some are not. But there are times when we use ‘some’ and don’t implicate that some are not. Suppose you’re talking to your mom, and you mention that you’re reading a logic book. For some reason, your mom’s always been curious about logic books, and asks you whether they’re a good read. (Just play along here) You respond, “Well, mom, I can tell you this for sure: Some logic books are boring. You should see this book I’m reading now; it’s a total snooze-fest!” In this case, you say that some logic books are boring based on your experience with this particular book, but you do not implicate that some logic books are not boring; for all you know, all logic books are boring—it’s just impossible to write an exciting logic book. This is a perfectly legitimate use of the word ‘some’, where all it means is that there is at least one: when you utter ‘some logic books are boring’, all you communicate is that there is at least one boring logic book (this one, the one you’re reading). This is a bit of natural-language unruliness that we must deal with: sometimes when we use the word ‘some’, we implicate that some are not; other times, we don’t, only communicating that at least one is. When we use ‘some’ in Aristotelian Logic, we need to know precisely what’s being said. So we choose: ‘some’ means ‘there is at least one’. ‘Some S are P’ tells us that those two classes have at least one member in common, and nothing more. ‘Some sailors are pirates’ means that there’s at least one sailor who’s also a pirate, and that’s it. There is no implication that some sailors are not pirates; at least one of them is, and for all we know, all of them are. (The justification for this choice requires an argument, which I will not make here. The basic idea is that the ‘some aren’t’ bit that’s often communicated is not part of the core meaning of ‘some’; it’s an implicature, which is something that’s (often, but not always) communicated over and above the core meaning.) This can confuse people, so it’s worth repeating. Heck, let’s indent it:
‘Some’ means ‘there is at least one’, and that’s it. It does not imply that some aren’t. With that out of the way, we can turn our attention to the Venn diagram for the particular affirmative. It makes the assertion that S and P have at least one member in common. Turning to our concrete example, the sentence ‘Some logicians are jerks’ makes the claim that there is at least one logician who is a jerk. (In fact, this is true: Gottlob Frege was an anti-Semitic jerk.) How do we draw a picture of this? We need to indicate that there’s at least one thing in the area of overlap between the two circles on the diagram—at least one thing inside of region 2. We do this by drawing an X: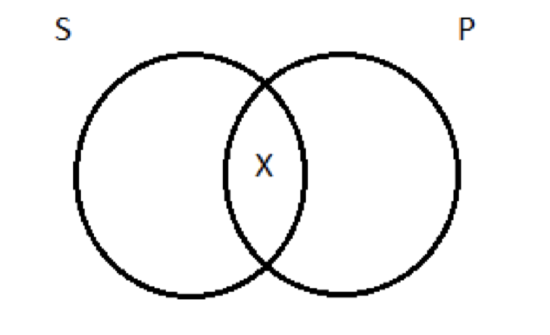 
Particular negative (O) This type of proposition denies that S is wholly included in P. It claims that there is at least one member of S that is not a member of P. Given that ‘some’ means ‘there is at least one’, the canonical expression of this proposition is ‘Some S are not P’—there’s at least one member of S that the two classes do not have in common. ‘Some sailors are not pirates’ expresses a true particular negative proposition; ‘Some dogs are not animals’ expresses a false one. The Venn diagram for O propositions is simple. We need to indicate, on our picture, that there’s at least one thing that’s inside of S, but outside of P. To depict the fact that some logicians are not jerks, we need to put Aristotle (again, not a jerk, I’m pretty sure) inside the S circle, but outside the P circle. As with the diagram for the I proposition, we indicate the existence of at least one thing by drawing an X in the appropriate place: 
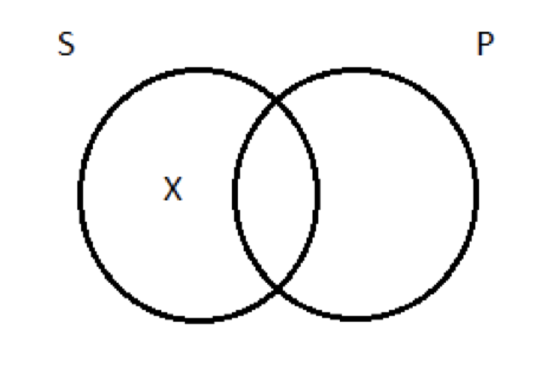A Note on Terminology It is commonly said that the four types of categorical propositions each have a quantity and a quality. There are two quantities: universal and particular. There are two qualities: affirmative and negative. There are four possible combinations of quantity and quality, hence four types of categorical proposition. The universal propositions—A and E, affirmative and negative—are so-called because they each make a claim about the entire subject class. If I claim that all hobos are whiskey drinkers, I’ve made an assertion that covers every single hobo, every member of that class. Similarly, if I claim that no chickens are race car drivers, I’ve made an assertion covering all the chickens—they all fail to drive race cars. The particular propositions—I and O, affirmative and negative— on the other hand, do not make claims about every member of the subject class. ‘Some dinosaurs were herbivores’ just makes the claim that there was at least one plant-eating dinosaur; we don’t learn about all the dinosaurs. Similar remarks apply to an O proposition like ‘Some dinosaurs were not carnivores’. Remember, ‘some’ just means ‘at least one’. The affirmative propositions—A and I, universal and particular—make affirmative claims about the relationship between two classes. A propositions affirm whole inclusion; I propositions affirm partial inclusion. Trivial fact: the Latin word meaning ‘I affirm’ is affirmo; the A and the I in that word are where the one-letter nicknames for the universal and particular affirmatives come from. The negative propositions—E and O, universal and particular—make negative claims about the relationship between two classes. E propositions deny even partial inclusion; O propositions deny whole inclusion. Trivial fact: the Latin word meaning ‘I deny’ is nego; the E and the O in that word are where the one-letter nicknames for the universal and particular negatives come from.
To tame natural language, Aristotelian Logic limits itself to that portion of language that expresses categorical propositions. Above, we gave “canonical” sentences for each of the four types of categorical proposition: ‘All S are P’ for the universal affirmative; ‘No S are P’ for the universal negative; ‘Some S are P’ for the particular affirmative; and ‘Some S are not P’ for the particular negative. These are not the only ways of expressing these propositions in English, but we will restrict ourselves to these standard forms. That is, we will only evaluate arguments whose premises and conclusion are expressed with sentences with these canonical forms. Generally speaking, here is the template for sentences qualifying as standard form: [Quantifier] Subject Term
This page titled 3.2: Classes and Categorical Propositions is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Matthew Knachel via source content that was edited to the style and standards of the LibreTexts platform.
